Scientific approaches often do not reflect the operational aircraft/airline conditions (e.g. seat load factor, conformance to the boarding procedure) or the non-deterministic nature of the underlying processes (e.g. amount and distribution of hand luggage). Furthermore, there is a clear lack of reliable data from aircraft operations and passenger handling. Assumptions regarding the inner processes are often derived from simplified research environments or gathered in less realistic test setups. To bridge this gap, data from the field are manually recorded during the day of operations to calibrate the passenger processes of a stochastic aircraft boarding model. The list of publications can be found here: references.
Boarding model
The proposed dynamic model for the boarding simulation is based on an asymmetric simple exclusion process (ASEP). The ASEP was successfully adapted to model the dynamic passenger behavior in the airport terminal environment. In this context, passenger boarding is assumed to be a stochastic, forward-directed, one-dimensional, and discrete (time and space) process. To provide both an appropriate set of input data and an efficient simulation environment, the aircraft seat layout is transferred into a regular grid with aircraft entries, the aisle(s), and the passenger seats. This regular grid consists of equal cells with a size of 0.4 x 0.4 m, whereas a cell can either be empty or contain exactly one passenger.

The boarding progress consists of a simple set of rules for the passenger movement: a) enter the aircraft at the assigned door (based on the current boarding scenario), b) move forward from cell to cell along the aisle until reaching the assigned seat row, and c) store the baggage (aisle is blocked for other passengers) and take the seat. The movement process only depends on the state of the next cell (free or occupied). The storage of the baggage is a stochastic process and depends on the individual amount of hand luggage. The seating process is stochastically modeled as well, whereas the time to take the seat depends on the already used seats in the corresponding row. The stochastic nature of the boarding process requires a minimum of simulation runs for each selected scenario to derive reliable simulation results. In this context, a simulation scenario is mainly defined by the underlying seat layout, the number of passengers to board (seat load factor, default: 85%), the arrival frequency of the passengers at the aircraft, the number of available doors (default 1 door), the specific boarding strategy (default: random) and the conformance of passengers in following the current strategy (default: 85%).
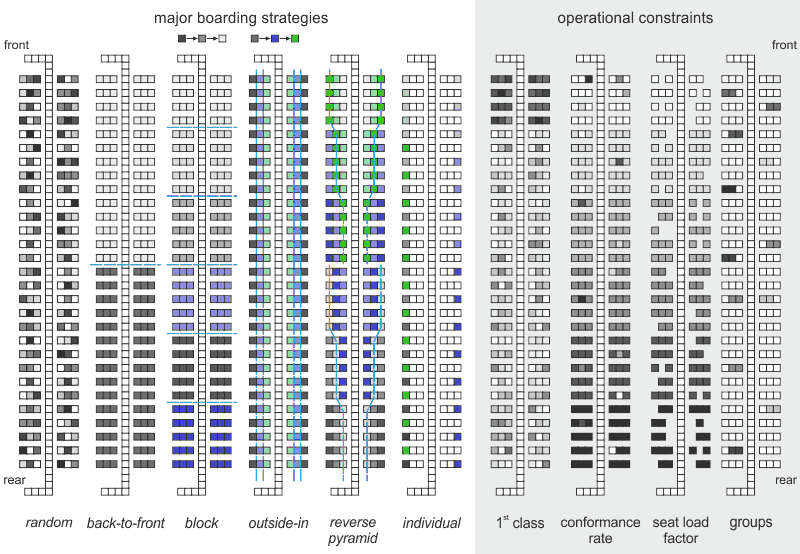
To model different boarding strategies, the grid-based ASEP approach enables an individual allocation of seats as well as an aggregation of seats to specific blocks according to specific boarding strategies. In general, boarding strategies follow three basic approaches: boarding per row, boarding per seat (window, middle, aisle), and sequences of specific seats. Here, six different boarding strategies are addressed: random, back-to-front, optimized block, outside-in, reverse pyramid, and individual seating. In the following figure, seats are color-coded to emphasize the order of boarding. For random boarding, passengers arrive with no specific chronological order. The back-to-front and the optimized block strategies consist of specific boarding blocks with different block sizes and order: back-to-front has two blocks and the rear block is boarded first, whilst the optimized block strategy has six blocks, which are alternately boarded (starting with the second last block). For the outside-in strategy, the seats are grouped into three blocks, which separate the window, middle, and aisle seats. Here, the window seats are boarded first, followed by the middle and the aisle seats. The reverse pyramid strategy is a hybrid approach of back-to-front and outside-in boarding and consists of eight blocks. Finally, the individual boarding strategy is a specific solution of the optimized block, since in this case, each block contains only one seat. Additionally, operational constraints are implemented into the model as well: 1st class seats, passenger conformance to boarding strategy, seat load factor, and group constellations.
Validation
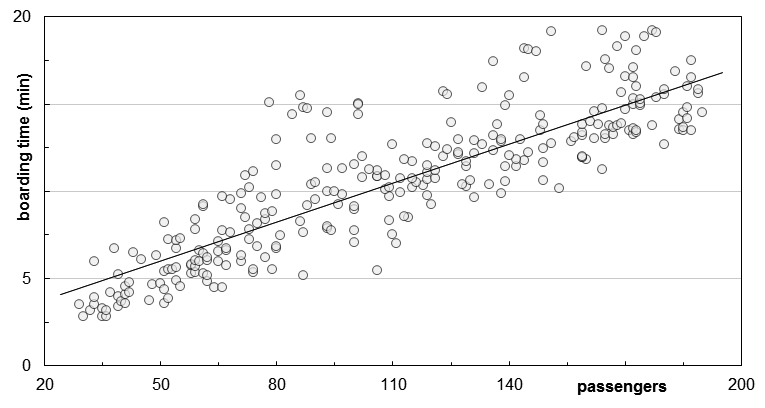
A reliable dataset for calibrating models for aircraft boarding is required, which covers a broad range of input factors. Even though experimental mock environments for individual setups or empirical analysis of specific elements of human behavior demonstrate the need for operational proofs. For this reason, in recent years data from more than 400 flights were manually recorded with a different focus and level of detail: passenger processes (e.g. time to store hand luggage or time needed to take the seat), arrival rates at the aircraft door, and boarding time using different boarding strategies. The recorded data are systematically analyzed and used to calibrate the input parameters of the boarding model and to validate the simulation results (boarding time and distribution). In the following figure, the measurements of manually measured 282 boarding events for single-aisle aircraft (Airbus 320, Boeing 737) are shown, with a minimum of 29 passengers and a maximum of 190 passengers. Assuming a linear boarding process, the boarding time increases for each passenger by 4.5 s, with an additional offset of 2.3 min on average (solid regression line).
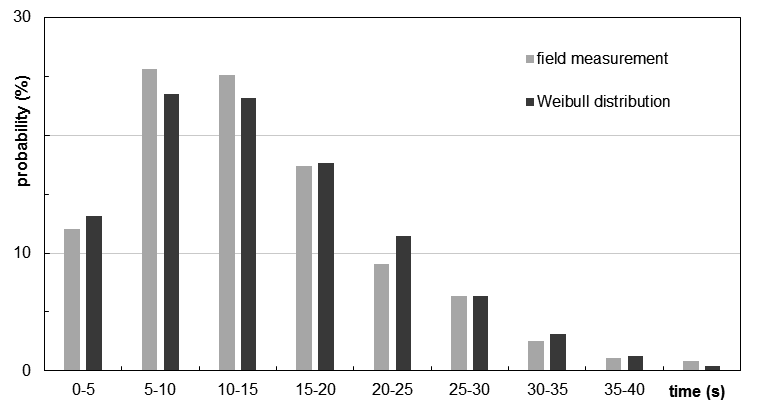
To calibrate the modeled passenger processes during boarding, the following input parameters were measured in the field: distribution of time needed to store hand luggage, distribution of time for seat shuffling (interactions during seating), distribution of passenger arrival rates at the aircraft door, and distribution of walking speed in the aisle of the aircraft cabin. Finally, the calibrated stochastic aircraft boarding model shows deviations smaller than 5% between measured and simulated boarding times.
Visualization
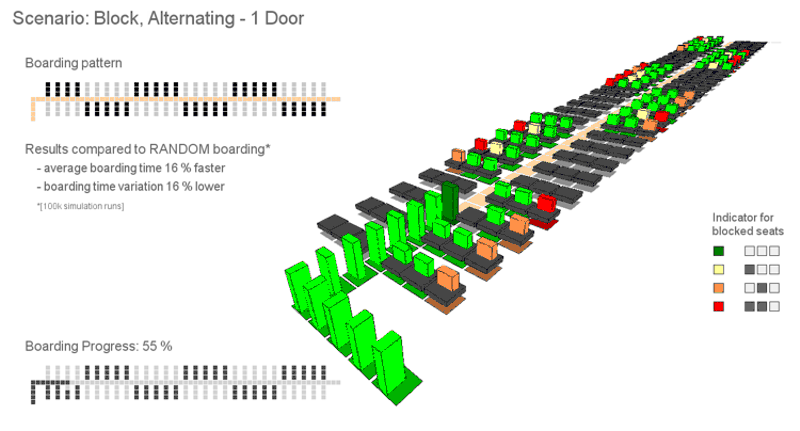
The stochastic boarding model is implemented in a simulation environment, which allows for evaluating specific boarding scenarios with different procedures and technologies. The model was primarily developed to analyze the A320 reference layout in an efficient way, by means of calculation times and consideration of relevant operational constraints. Nevertheless, the model was extended to be used for twin-aisle configuration, implementation of infrastructural changes such as the Side-Slip Seat, development and optimization of appropriately adapted boarding strategies, and to derive a complexity metric to predict boarding progress. An additional visualization module is developed to demonstrate the working principle of the analyzed boarding scenarios.
References
- Michael Schultz (2018). Implementation and application of a stochastic aircraft boarding model
- Michael Schultz (2018). Field Trial Measurements to Validate a Stochastic Aircraft Boarding Model
- Michael Schultz (2018). Fast aircraft turnaround enabled by reliable passenger boarding
- Michael Schultz (2017). Aircraft Boarding – Data, Validation, Analysis
- Michael Schultz, Thomas Kunze, Hartmut Fricke (2013). Boarding on the critical path of the turnaround
- Michael Schultz, Christian Schulz, Hartmut Fricke (2008). Efficiency of Aircraft Boarding Procedures
The complete list of publications can be found here: references.
